[Yongggg's] Partial Dependence Plot의 이해

안녕하세요 Yonggg's Blog입니다! 오늘 설명드리고자 하는 것은 Partial Dependence Plot 입니다.

1. 목적

저번 시간 다루었던 Feature Importance와 비슷하게 Partial Dependence Plot 또한 변수의 중요도를 파악하는 개념이다.

2. 개념

특정 변수 부분집합과 예측 사이의 함수 관계를 나타냄으로써 알아낼 수 있다.  Target 값에 영향을 주는지 안 주는지 알고 싶은 변수의 부분집합을 특정값으로 고정시킨 후(ex: 부분집합 변수가 1개일 때, $ X_{s} $ = {50}), $ f(X_{s}, X_{c}) $에서 $ X_{c} $에 해당하는 Feature의 모든 샘플(obs)에 대해 기대값을 취하여 $ \hat{f}_{X_{c}}(x_{c}) $값(Target 예측값)을 구하고, 이를 $ X_{s} $가 Sample에 존재하는 모든 경우에 대해서 기댓값을 구한 뒤, 기댓값들을 Plot으로 나타내는 것이다.

 

3. 원리

여러개의 Feature 중, 우리가 관심이 있는 Feature Subset을 $ X_{s} $로, 나머지 Feature의 여집합을 $ X_{c} $라고 했을때, ($ X^{T} = (X_{1}, \cdots , X_{p} ), X=X_{s} \cup X_{c} $로 나타낼 수 있고, S : subset은 시각화의 편의성 때문에 1개 또는 2개로 구성한다.)

 

이때 우리가 학습한 모델을 $ f(X) (=f(X_{s}, X_{c})) $로 나타낼 수 있다. 그리고 $ X_{s} $에 대해 Partial dependence를 취하면, (회귀 모형에서는 $ X_{s} $를 고정 한 뒤, 나머지 Feature $ X_{c} $에 대해서 $ f(X_{s}, X_{c}) $의 Expectation을 취한다. 이를 (수식 1)로 표현할 수 있다.

$$ f_{X_{s}}(X_{s}) = E_{X_{c}}[f(X_{s}, X_{c})] \quad (수식 1) $$

(수식 1)의 Expectation 식을 Summation과 Integral로 표현하면, (수식 2)처럼 나타낼 수 있다.

$$ E_{X_{c}}[f(X_{s}, X_{c})] = \int f(X_{s}, X_{c})f_{X_{c}}(x_{c})dx_{c} \quad or \\ E_{X_{c}}[f(X_{s}, X_{c})] = \sum f(X_{s}, X_{c})f_{X_{c}}(x_{c}) \quad (수식 2) $$

$$ where f(X_{s}, X_{c}) \; is \; model, \; f_{X_{c}}(x_{c}) \; is \; probability \; density \; function \; (pdf) $$

 

이 때, 모든 X_{s}의 경우의 수에 대하여 위의 Eepectation 값을 구한 뒤 Plot을 그리면, Partial Dependence Plot이 된다.

 

이산형 자료를 예로 들어 설명해 보겠다.

알기 쉽게, 물과 가스를 쓴 양으로 세금을 예측하는 문제라고 정의해보겠다. '$ f(물, 가스) = 세금 $'

이 때, 물의 사용량만의 영향을 보는 것에 관심이 있다고 한다. 모든 모집단에 대해서 가스 사용량의 분포를 안다고 가정했을 때, (주어진 물의 사용량, 가스 사용량)에 대한 모든 경우의 수를 키의 Probability Density Function을 반영해 Expectation을 취해보겠다. 만약 가스 사용량의 모집단 분포가 다음과 같고, 주어진 가스 사용량이 50이라면, 

 

X	100	200	300	400
$ p (가스 사용량 = x) $	$ { 1 \over 2 } $	$ { 1 \over 4 } $	$ { 1 \over 8} $	$ { 1 \over 8} $
$f(물 =50(고정), 가스=x)$ (세금 예측 값)	1000	1200	1600	1400

 

$ E[f(물 = 50)] = 1000 \times { 1 \over 2} + 1200 \times { 1 \over 4 }  + 1600 \times { 1 \over 8 } + 1400 \times { 1 \over 8 } = 1175 $이다. 

(실제 $X_{s}, \; W_{c}$의 모집단은 알 수 없기 때문에 $ f_{X_{c}}(x_{c}) $도 당연히 할 수 없으나 train set의 데이터들로 모집단의 P.D.F를 추정하여 사용한다. 또한 $ f $는 단순 $ X $로 학습한 모델이며, $ \hat{f}_{X_{s}}(X_{s}) $는 $ f $에 고정 값 $ X_{s} $와 모든 $X_{c}$의 샘플 값 를 넣은 것이다.)

 

이를 수식으로 요약하여 나타내면, (수식 3)처럼 나타낼 수 있다.

$$ \hat{f}_{X_{s}}(X_{s}) = { 1 \over n } \sum_{i}^{n}f(X_{s}, x_{ic}) \quad (수식 3)$$

 

만약, 물의 사용량이 50, 100, 150, 200이 존재한다면, 이 4가지 경우에 대해 위와 같은 방법으로 4가지 경우의 Expectation Value를 구한다. 이를 물의 사용량을 X축으로, Expectation Value를 y축으로 설정하면, 우리가 원하는 Partial Dependence Plot을 그릴 수 있다.

 

[그림 1]은 필자가 2021.01 해커톤에서 이 방법을 사용하여 Feature Importance를 구한 예시이다. 모델로 Target을 예측할 뿐만 아니라, PDP로 변수의 중요도까지 나타냈고 제조업의 상품설계를 도왔다. 이렇듯 다양한 도메인에서도 적용이 가능하다는 점이 장점이다.

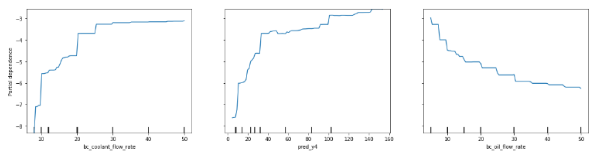
[그림 1] PDP plot

4. 주의 사항

이때, $ X_{s} $와 $ X_{c} $는 상관관계가(다중공선성) 없는 변수로 구성되는 것이 좋다. (상관 계수가 크다면, $X_{s}$를 고정했을 때, $ X_{c} $에서 $ X_{s} $의 역할을 대신 할 것이기 때문이다.)

또 Expectation은 상위에 있는 값들과 하위에 있는 값들이 대칭성을 띄며 존재한다면, 그에 대한 기대값은 0으로 나와, Feature의 효과가 없는 듯 보이지만, 사실은 양 극단에 분포하여 영향을 줄 수 있다.

 

이렇게 Partial Dependence Plot의 개념을 알아보았습니다. 논문에 기술된 통계적 내용은 생략하여 적어놨습니다. 혹시 관심이 있으시다면 논문을 참고해주시기 바랍니다.^^ 감사합니다!