-
[yongggg's] Audio Domain (소리의 기초)domain 2025. 4. 23. 09:53
* 소리의 기초
(1) Sound
소리는 일반적으로 진동으로 인한 공기의 압축에서 생성된다.
(2) Wave
공기의 압축이 얼마나 됐는지에 따라 표현한 것을 wave(파동)이라고 한다. $/rightarrow$ 파동은 진동 하며, 공간(매질)을 전파해 나가는 현상이다.
(3) Frequency(주파수)
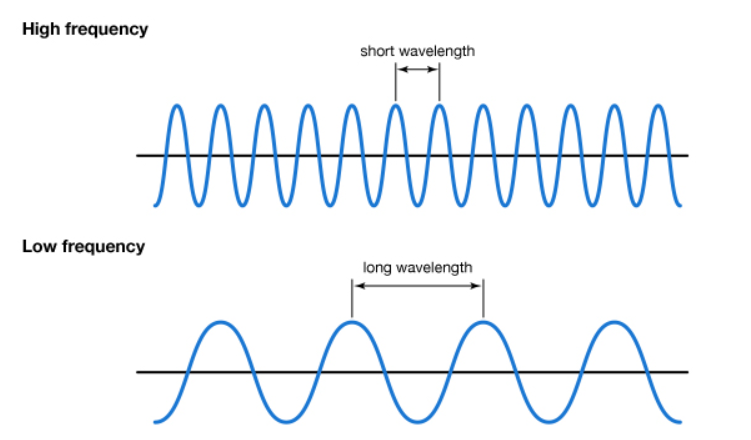
파동의 초당 진동수를 주파수라고 하며, 헤르츠(Hz) 단위로 표기한다.
소리가 얼마나 압축되어 있는지를 나타내며, 1초 동안의 진동 횟수를 나타낸다.주파수가 높다면, 높은 소리를 내고 낮다면, 낮은 소리를 낸다.
[source] https://kids.britannica.com/students/assembly/view/223513 주파수는 다음 세 가지의 요소를 가진다.

[source] https://www.youtube.com/watch?v=Z_6tAxb89sw (4) Amlitude(진폭)
소리의 크기와 관련이 되어 있는 요소이다. 진폭이 클수록 큰 소리가 되며, 작을수록 작은 소리가 된다.
"bel"이라는 소리 크기(음압)에 대한 단위를 사용하며, 실제 사용 시에는 bel 값에 10을 곱한 decibel(dB)을 사용한다.
[source] https://blog.naver.com/PostView.nhn?blogId=papers&logNo=221236649396 (5) Tone Color, Timbre(음색)
음색은 소리의 고유한 특성으로, 같은 음높이(주파수)와 음량(진폭)을 가진 소리라도 서로 다르게 만드는 질적인 특성이다.
이 음색은 기음/기본 주파수, 배음/고조 주파수, 공명 등으로 결정 지어진다.- 기음 / 기본 주파수 : 소리의 높낮이를 구분할 수 있는 기본이 되는 주파수
- 배음 / 고조 주파수 : 기음의 정수배가 되는 주파수

[source] http://contents.kocw.or.kr/document/03_Sound.pdf (6) Phase; Degress of displacement(위상)
소리와 같은 파동은 시간에 따라 진동하는데, 이 진동은 주기성을 가진다. 위상은 이 주기적 파동이 주기의 어느 지점에 있는지를 나타내며, 각도(degrees) 또는 라디안(radian) 단위로 표현된다.
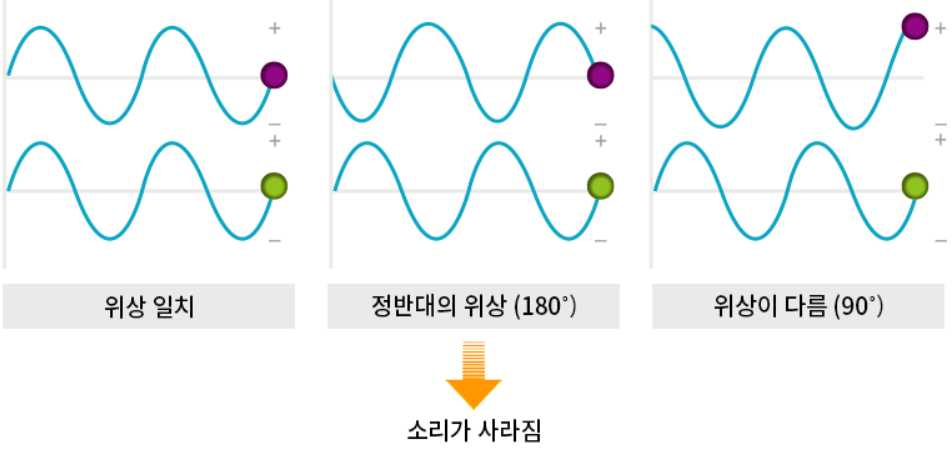
[source] http://www.sorishop.com/board/special/board_view.html?no=565&s_field=memo&s_key=%B3%F4%C0%BA&page=3
* Audio Analysis
(1) Sampling
자연에서 오는 소리(아날로그 데이터)를 컴퓨터에서 사용하기 위해, 우리는 숫자화(디지털화)를 해야한다.

[source] https://evan-moon.github.io/2019/07/10/javascript-audio-waveform 컴퓨터는 연속적인 아날로그 신호를 특정 시간에 전기 신호를 측정하고 그 값을 저장하는 방식으로 데이터를 저장한다.
이 때 측정하는 특정 시간을 세밀하게 둔다면, 원래 신호와 더욱 가까워 질 수 있다.
(2) Sample rate
sampling 시 특정 간격을 의미한다. sample rate가 높을수록 음질이 좋은데, 특히 높은 주파수를 가진 소리(고음)의 해상도가 좋아진다.

[source] https://evan-moon.github.io/2019/07/10/javascript-audio-waveform 인간이 들을 수 있는 주파수는 20hz ~ 20khz 이며, 보통 CD에서 사용하는 sample rate는 44.1khz이다.
왜 사람이 들을 수 있는 주파수에 두 배 가량을 녹음 기록에 사용하는지에 대해 궁금증이 생길 것이다.

[Sourc] https://evan-moon.github.io/2019/07/10/javascript-audio-waveform/ 여기서 그래프가 x축 위로 나와있는 (+) 부분이 공기 압축을 나타내며, x축 밑으로 들어가 있는 (-) 부분이 공기 팽창을 나타낸다.
인간은 소리를 들을 때, 압축 $\rightarrow$ 팽창 $\rightarrow$ 압축까지 모두 들어야 공기의 떨림(소리)를 느낄(들을) 수 있다.
이 과정에서, 인간이 들을 수 있는 가장 높은 소리(20khz)를 측정하려면, 20khz $\times$ 2 = 40khz 를 측정해야 한다.
하지만, 이 보다 더 높은 사이클을 갖는(예를 들어 30khz) 주파수가 들어온다면, 녹음할 때 들리지 않았던 소리가 들리게 된다. 이 현상을 Ghost Frequency라고 부른다.
위 문제를 해결하기 위해 낮은 주파수만을 통과시키는 LPF(Low Pass Filter) 방법을 사용하는데, 녹음 시 LPF를 사용하여 가청주파수보다 높은 소리는 자르고 인간이 들을 수 있는 소리만 통과시키는 것이다.

[source] https://evan-moon.github.io/2019/07/10/javascript-audio-waveform (3) Feature Extraction
원시 오디오 신호(예: 음파의 진동 데이터)에서 의미 있는 정보를 추출하여, 이를 수치적/구조적 형태로 변환하는 과정을 말한다. 아래와 같이 wave form 형태의 데이터는 시간 축과 주파수 축으로 구성된다. 이런 wave form의 데이터로 부터 의미있는 Feature를 추출하는 것이 목적이다.
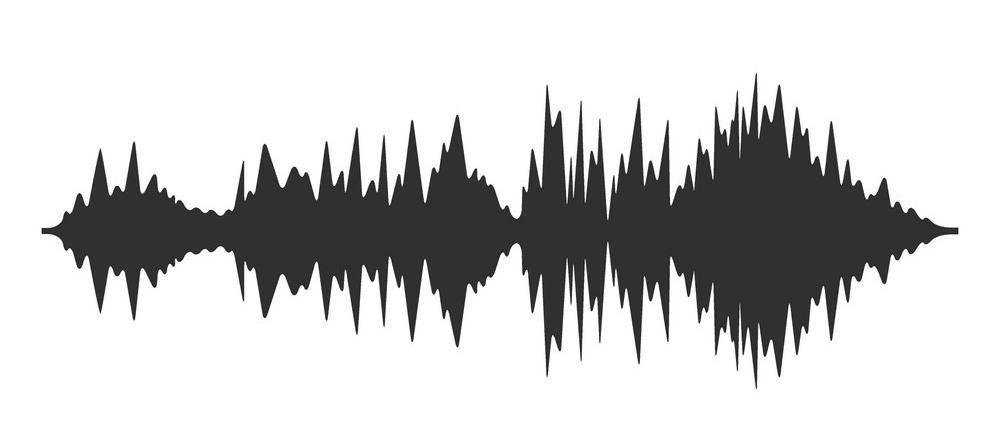
[source] https://www.vectorstock.com/royalty-free-vector/audio-wave-high-quality-vector-42958791 (3-1) Fourier Transform (푸리에 변환)
Fourier Transform은 Continuous Signal을 주파수 도메인으로 변환하는 수학적 연산이다. 이 변환은 입력 오디오 신호를 다양한 주파수를 갖는 주기 함수들의 합으로 분해하여 표현해준다.
즉, 고주파부터 저주파까지의 대역을 가진 sin / cos 함수로 원본 신호를 분해한다.

[source] https://ww2.mathworks.cn/help/signal/ref/stft.html 푸리에 변환이 연속 시간 신호를 주파수로 변환하는 이론적 도구 이지만, 실제 환경은 디지털 환경이기 때문에 이를 직접 사용할 수 없다. 따라서 컴퓨터가 계산이 가능하도록 하게 하는 DFT를 사용한다. 따라서 DFT(Discrete Fourier Transform)은 시간 및 주파수의 특정 지점에서 크기와 위상을 알 수 있다.
자세한 내용은 https://youtu.be/spUNpyF58BY?t=491 에 알기 쉽게 설명되어 있다. (이것도 되게 어려운 내용이지만, 아무것도 모르는 입장에서 보기 편함.)나아가, 요즘은 Fast Fourier Transform 방법을 사용하는데, 이는 DFT를 효율적으로 계산하기 위한 계산 방법이다.
(3-2) Spectrum (스펙트럼)

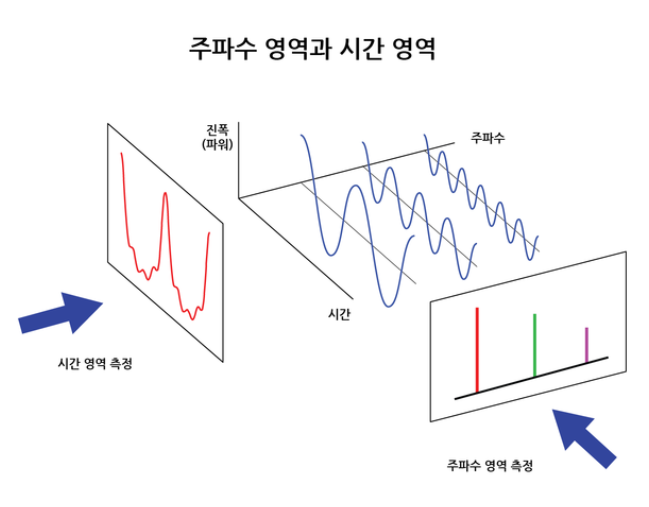
[source] https://ratsgo.github.io/speechbook/docs/fe/mfcc 푸리에 변환을 실시한 결과물을 그래프로 나타낸 것을 spectrum이라고 한다. 즉, 파동의 시간 도메인을 주파수 도메인으로 변환한 것이다.
이 그래프를 보면, 음향 신호를 주파수 및 진폭으로 분석하여 볼 수 있지만, 시간에 대한 정보는 없다. (x축은 주파수, y축은 진폭)
[source] https://m.blog.naver.com/novatest/221460293414 위의 그림에서 붉은색으로 표시된 입력 신호가 들어가면, 푸리에 변환을 거친 파란색의 주기 함수 성분들이 나온다. 이 파란색 주기 함수 성분들은 각각 고유한 주파수를 가지고 있으며, 이들을 모두 더하면 붉은색인 입력 신호가 된다.

[source] https://blog.naver.com/intknk2/221406515869 FFT를 통해 변환된 그래프는 신호의 주파수 성분이 hz로 이루어져 있다는 사실만 알 수 있으며, 주파수 성분이 어느 시점에 존재하는 지는 알 수 없다. 이 시점은 복잡한 신호일수록 더 알기가 어렵기 때문에 이를 알 수 있는 Time-Frequency의 영역의 분석 방법인 "STFT"가 생겼다.
(3-3) Short-Time Fourier Transform
STFT는 (3-2)에서 언급한 이유 때문에 생겼으며, 시간 도메인의 signals를 시간-주파수 도메인으로 변환하도록 한다. 방법을 간단히 설명하면, 신호를 작은 시간 구간으로 나눈 뒤, 각 구간에 대해 개별적으로 Fourier 변환(컴퓨터 영역에서는 DFT)을 수행하여 시간-주파수 표현을 얻는다.

https://kr.mathworks.com/help/dsp/ref/dsp.stft.html 이 변환은 짧은 window를 설정했을 때, 시간 해상도는 높아지지만 주파수 해상도가 낮아진다는 trade off를 갖는 것이 특징이다. 따라서 overlap을 통해 이러한 trade off를 보완할 수 있다. 아래 그림은 이 STFT 결과를 보여준다.

https://en.wikipedia.org/wiki/Short-time_Fourier_transform (3-4) spectrogram (스펙트로그램)
위의 (3-3) STFT 작업을 거치고, 이를 이어 붙여 최종적으로 audio signals의 시간-주파수로 표현한 것이 Spectrogram이다.
Spectrum은 파형 전체를 대상으로 특성을 분석했다면, Spectrogram은 STFT의 프레임을 작게 쪼갠 것을 조금씩 이동하면서 이어 붙였다.
이를 visualIzation 하면 아래의 히트맵과 같다. x축은 시간(Time), y축은 주파수(Frequency), z 축은 특정 시간, 특정 주파수의 진폭을 나타내며, 진폭의 차이를 색상의 진하기로 나타낸다.

[source] https://sswwd.tistory.com/2 또, 이렇게 위의 그래프와 동일한 데이터는 아니지만 3차원으로 표현했을 때의 예시를 다음과 같이 생각해볼 수 있다.

[source] https://www.faberacoustical.com/apps/ios/signalscope_adv_2018 (3-5) Mel-Spectrogram
(3-4)에서 Spectrogram을 구했다면, Mel-Spectrogram은 인간의 청각 특성에 맞게 변환한 시간-주파수 표현이다. Spectrogram이 시간과 주파수에 따른 신호의 크기를 나타낸다면, Mel-Spectrogram은 주파수 축을 Mel-scale로 변환하여 인간이 주파수를 인지하는 방식에 더 가까운 표현을 제공한다.
Mel-Scale이란 다음과 같이 구할 수 있으며, 이 공식은 저주파수에는 선형적이고, 고주파수에서는 로그적으로 변화하여 인간의 청각특성을 반영한다.
$$ m= 2595 \log_{10} \left( 1 + {f \over 700} \right) $$
이 외에도 Feature Extraction의 방법은 다양하게 존재한다.

[source] librosa official site