Basic Contents of Reinforcement Learning 2

이전 장에서 다루었던 강화학습의 기초를 바탕으로 다시 한번 내용을 정리하고자 합니다. (봐도 봐도 헷갈리고 어렵네요...)

Agent

강화학습에서 Agent는 관측을 하고, 주어진 환경에서 행동을하며, 이 행동의 결과로 보상을 받는다.

이 Agent의 목적은 보상의 장기간 기대치를 최대로 만드는 행동을 학습하는 것이다. (목적지에 도착하면 양의 보상, 시간을 낭비하거나 잘못된 방향으로 향하면 음의 보상을 받는 방식으로 보상을 설정함)

Reinforcement Learning

강화학습은 위의 Agent가 주체가되어 행동 $\rightarrow$ 상태 변화 $\rightarrow$ 보상의 학습의 순환 구조를 갖는다.

Agent가 행동을 결정하기 위해, 사용하는 알고리즘을 Policy(정책)이라고 한다. (요새 핫한 인공지능 신경망은 관측을 입력받고 수행할 행동을 출력하기 때문에 Policy(정책) 그 자체가 될 수 있다.)

이 정책을 결정하는데에는 다음과 같이 두 가지 방법이 존재한다.

• 탐험형 정책(exploration policy)
  $\rightarrow$ 이 방법은 처음부터 끝까지 무작위로 선택하는, 즉 매번 다른 경우의 수를 선택하고 가장 성능이 좋은 조합을 고르는 방법(ex: random 알고리즘)
• 탐사형 정책(exploitation policy)
  $\rightarrow$ 기존의 경험을 토대로 가장 최대의 보상을 얻을 수 있는 행동을 수행하는 방법(ex: greedy 알고리즘)

탐험을 통해 얻은 결과는 항상 정답이 아니기에 낭비가 일어나며, 풍부한 경험을 통해 좋은 선택을 할 수 있지만, 경험을 풍부하기 만들기 위해서는 새로운 시도를 해야하며, 새로운 시도는 늘 위험 부담을 갖고 있다.

이 때, 최적의 정책은 충분히 긴 episode를 통해 최적 정책을 얻어낼 수 있는데, 이는 시간 및 비용이 비효율 적인 경우가 많다. 따라서 탐험형과 탐사형 정책의 균형이 매우 중요하다. 

 

강화 학습에서 보상을 최대화할 수 있는 방향으로 탐험과 탐사 사이의 적절한 균형을 맞추는 데 사용되는 의사 결정 프로세스는 대표적으로 MDP(Markov Decision Process)가 있다.

Markov Decision Processes

모든 state(상태)는 그 직전의 상태와, 그 상태에서만이 Agent가 선택한 행동이 도출한 결과이다. 또, $t-1$의 상태는 $t-2$ 시점의 state와 $t-2$ 시점의 상태에서 한 행동이 도출한 결과이다. 이렇게 $t-2$, $t-3$의 결과들을 따라가보면, 처음 시작했던 시점까지 갈 수 있을 것이다. 이렇게 연결되어 있는 모든 단계들과 그 순서는 현재 $t$시점의 현재 상태를 결정짓는 정보를 담고 있을 것이며, 그에 따라 지금 순간 Agent가 어떤 행동을 선택해야하는지에 대해서도 직접적인 영향을 미친다. 즉, 모든 정보들을 활용한다면, Agent가 어떤 선택을 해야하는지 결정하는 데, 큰 도움이 될 것이다.

하지만 이렇게 된다면, Agent가 한 단계씩 나아갈 때마다, 점점 더 많은 정보들이 저장되어야 하며, 그 양은 계속 늘어난다. 이렇게 많은 양의 데이터를 다루면서 연산하는 것은 쉽지 않다. 그래서 MDP를 가정하고, 현재 $t$시점의 state는 $t-1$시점의 state와 action에 따라 결정한다고 가정한다.

$$ r(s,a) = E[R_{t} | s_{0}, a_{0}, s_{1}, ..., s_{t}, a_{t}] = E[R_{t} | s_{t}, a_{t}] $$

The Bellman Equation (벨만 방정식)

이제, 위의 개념을 토대로 강화 학습을 본격적으로 한다고 생각하면 된다. 먼저, 우리는 모든 state에서 취해난 각각의 행동에 대해 보상을 얼마나 받는지 미리 알고 있다고 하자. 그럼, state마다 가장 높은 보상을 받을 수 있는 행동들을 연속적으로 취하면 될 것이다. 이렇게 최종적으로 받는 모든 보상의 총합을 Q-value(Quality Value)라고 한다.

$$ Q(s,a) = r(s,a) + \gamma \max\limits_{a} Q(s^{'}, a) $$

상태 $s$에서 행동 $a$를 취할 때, 받을 수 있는 모든 보상의 총합 $Q(s,a)$는 현재 행동을 취해서 받을 수 있는 즉각 보상 $r(s,a)$와 미래에 받을 미래 보상의 최대값 $\gamma \max\limits_{a} Q(s^{'},a)$의 합으로 계산할 수 있다. 여기서 $s^{'}$는 현재 상태 $s$에서 행동 $a$를 취해 도달하는 바로 다음의 상태로 $\max\limits_{a} Q(s^{'}, a)$는 다음 상태 $s^{'}$에서 받을 수 있는 보상의 최대값이다. 이 값을 최대화 할 수 있는 행동을 선택하는 것이 Agent의 목표이다. 그리고 그 앞에 있는 $\gamma$는 할인율이라고 불리며, 미래가치에 대한 중요도를 조절한다. $\gamma$값이 커질수록 미래에 받을 보상에 더 큰 가치를 두는 것이고, 작아질수록 즉각보상을 더 중요하게 고려한다.

- 이때, 필자는 딥러닝 학습만 해보았던 사람이기 때문에, 미래의 보상을 어떻게 알고 또, 어떻게 학습에 반영할지 생각을 해봤다. 다음의 생각은 FrozenLake 문제일 때이다.

먼저, 첫번째 시도(에피소드)에서 Initalization된 policy에 따라 Agent가 움직이는데, 최초로 Goal에 달성할 때까지는 policy의 업데이트는 일어나지 않는다. 최초 Goal에 달성했을 때 비로소 이전 cell에서 Goal로 가는 방향으로 가중치가 업데이트가 될 것이다. 그렇다면, 다음 episode에서 Goal로 가기전의 2-step 이전의 cell에서는 1-step 이전의 cell에서 Q value가 등장하게 되며, 2-step 이전의 cell의 policy가 업데이트 된다. 이렇게 연쇄적으로 episode가 반복됨에 따라, policy는 업데이트 된다.

이 벨만 방정식은 다음 두가지의 성질로 인해, 강화학습에서 굉장히 유용하다.

- Markov stage 가정이 유효하다고 가정했을 때, 벨만 방정식의 재귀적인 성질은 미래에 받을 수 있는 보상을 멀리 떨어진 과거로까지 전파될 수 있게 한다.

- 또한, 벨만 방정식의 재귀적은 성질은 처음의 실제 $Q$ 값이 얼마인지 알지 못해도 괜찮도록 한다. $\rightarrow$ 처음에는 추측으로 값을 정하지만, 점점 수렴해서 마지막에는 정답 값에 도달할 것이다.

Q-Learning

위으 방정식까지의 내용에서, 강화 학습의 목적은 "가장 높은 누적 보상을 얻을 수 있는 행동을 한다." 라는 기본 전략이 생겼다. 매 순간 가장 보상이 높을 것이라는 행동을 취한다는 점에서, greedy 알고리즘이라고 부르기도 한다.

이런 전략은 다음 그림과 같이, 보통 모든 가능한 상태-행동 조합을 표로 그린 후, 거기에 모든 Q-value를 적어 사용하는 것이다. 그 후에는 벨만 방정식을 이용하여, 표를 점점 업데이트할 수 있다.

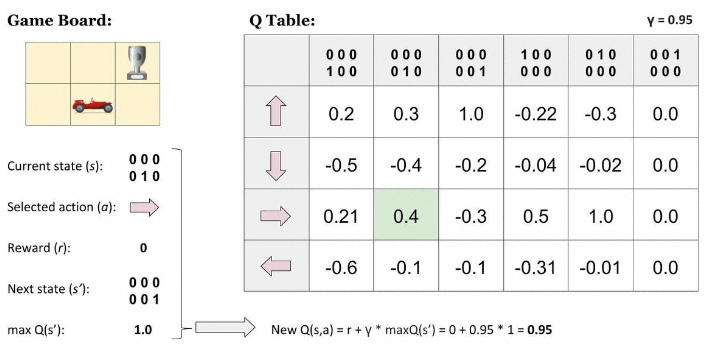
업데이트는 위의 그림에서, 초록색으로 칠한 자리인 0.4라는 확률을 다음 공식을 이용해 0.95로 업데이트할 수 있다.

$$ Q(s,a) := r(s,a) + \gamma \max\limits_{a} Q(s^{'}, a) $$

여기서 ':=' symbol은 '같다'가 아닌 '할당한다'라는 의미로 사용했다.

 

Agent가 가장 오른쪽 위 칸에 도달하면 게임이 끝난다. 즉, 표에서 맨 오른쪽 열이 나타내는 상태는 종결상태이다. 이 상태에서 Agent는 아무런 행동 또는 상태 변화를 할 수 없기 때문에 모든 값은 0이다. 그렇다면, 종결상태인 $s^{'}$에 도달하기 직전의 상태에 대해서는 단순히, 그다음 순간 받을 즉각 보상으로만 가치를 산정할 수 있다. 

$$Q(s,a) = r(s,a)$$

 

여기서 문제가 복잡했을 때, greedy 알고리즘의 문제점은, 항상 '최선의 선택'만을 한다는 것이다. 이렇게 되면, 새로운 선택을 해보지 않게되고, 그렇게 되면, 아직 받아보지 못한 미지의 보상에 대해서는 앞으로 그 존재를 알 수 없을 것이다.

이 문제를 해결하기 위해, $\epsilon - greedy$ 전략을 추가한다. 바로 $0 < \epsilon < 1$인 어떤 $epsilon$값을 이용해서, 탐험과 활용을 적절히 번갈아가며 사용하는 것이다. $ p = 1 - \epsilon$의 확률로는 원래 했던 대로 greedy하게 행동을 하고, 나머지 $p= \epsilon$의 확률로는 랜덤으로 행동을 취하는 것이다. 이렇게 함으로써 Agent는 새로운 공간으로의 탐험을 하면서, 알지 못하는 것들도 놓치지 않게 학습할 기회를 갖게된다.

이 알고리즘을 바로 Q-Learning이라고 한다. (간혹, 표를 이용한다고 하여 Q-table이라고도 한다.)

Deep Q Networks

현실 세계에서는 위에서 언급한 행동 및 상태 등이 매우 방대해질 수 있다. 이제 Q-table로는 담을 수 없는 양이 형성되며, Q-table 대신 딥러닝 모델을 사용하게 됐고, Q-Learning 과 Deep-Learning을 합친 것을 Deep Q Networks라고 한다.

이 모델은 approximator(근사기), 또는 approximating function(근사 함수)라고 부르기도 한다. 모델에 대한 표현은 $Q(s,a; \theta)$라고 하고, 여기서 $\theta$는 신경망에서 학습할 가중치를 나타낸다.

위의 벨만 방정식에서 $=$의 기호는 '할당'이라는 의미를 가진다. 이 때, 좌변과 우변이 실제로 같아지는 순간은 언제일까? 바로 $Q-value$가 수렴하여 참값에 도달했을 때, 두 값은 완전히 같아진다. 우리가 학습시키고자 하는 최종 목적지 또한 바로 이 것이다.

이런 메커니즘으로 보았을 때, Deep Q Learning의 목적함수는 다음과 같은 식으로 정리할 수 있다.

$$ cost = \left[ Q(s,a; \theta) - \left( r(s,a) + \gamma \max\limits_{a} Q(s^{'}, a; \theta) \right) \right]^{2}$$

이 식은 Mean Square Error function이며, 현재 Q-value를 예측값 $y$라고 하고, 벨만 방정식의 우변에서 계산된 즉각 보상과 미래 가치의 합을 $y^{'}$라고 한다면, 다음과 같은 식으로 표현될 수 있다.

$$ MSE= {1 \over n} \sum^{n}_{1} (y_{i} -y^{'}_{i})^{2}$$

이런 성질 때문에 $Q(s^{'}, a; \theta)$는 Q-target 이라고 불리기도 한다.

 

이제 학습 과정에 대해 살펴보자. 강화학습에는 Training Datase이라는 것이 따로 없다. Agent가 행동을 취함에 따라 Dataset은 점점 쌓여나가는 것이다. Agent는 매 순간 그때까지 학습된 네트워크를 통해 최적이라고 판단된 행동을 취하며, episode가 끝날 때까지 상태, 행동, 보상, 그리고 다음 상태에 대한 데이터를 쌓아나간다.

 

데이터를 쌓으면서 학습하는 과정은 다음과 같다. 학습에 필요한 batch size를 $b$라고 한다면, Agent는 행동을 $b$번 취하며, $b$개의 Dataset들을 기록한다. 여기서 요점은 저장되어 있는 메모리 공간에서 방금 기록된 $b$개의 Dataset으로 학습하는 것이 아니라, 지금까지 쌓인 Dataset 중 $b$개를 랜덤으로 선택하여 신경망을 학습한다는 것이다. (DeepMind의 David Silver는 직전에 쌓인 $b$개의 Dataset을 그대로 사용하면, 그 데이터 간에는 상관관계가 너무 크기 때문에 학습이 제대로 이루어지지 않아서, 랜덤으로 추출한 데이터셋으로 학습을 시킨다고 한다.)

 

다음으로 모델 구조에 대해 살펴보자. 위에서 봤던 단순한 Q-table 방식은 현재 상태와 현재 취할 행동, 이 두가지를 입력으로 받는다. 그 후에는 모델 내 연산을 거쳐 Q-value를 출력한다. 이는 다음 그림과 같다.

하지만, 여기서 고려해야할 사항이있다. 위의 구조는 비효율 적인 면이 있는데, 벨만 방정식에서 value를 최대화하기 위해 미래에 선택할 수 있는 행동에 따른 가치 중 최대값을 취해야하는 부분이 있었다. $\max\limits_{a} Q(s^{'}, a)$ 부분이다. 그렇다면, 최대 값을 찾기 위해서는 모든 행동을 취해봐야 알 수 있다. 즉, 신경망 연산을 여러번 돌려야한다는 것이다. 이에 대한 비효율적인 부분을 다음과 같은 구조로 변형하여 효율적으로 바꿀 수 있다.

모델을 이렇게 수정해준다면, 모델에 상태를 입력으로 주었을 때, 각 행동에 대한 모든 Q-value를 한 번에 얻을 수 있다.

Double Deep Q Learning

위에서 Deep Q Networks의 목적함수와 MSE를 비교했다. MSE는 정답값 $y$와 예측값 $y^{'}$를 비교했다. 여기서 보통의 기계학습에서 정답값 $y$는 학습을 하는 과정 중 변하지 않는 상수값이지만, Deep Q Networks에서는 $y$와 $y^{'}$ 모두 신경망이 출력하는 값이기 때문에, 매 학습 단계마다 target이 움직일 수 있다. 이로 인해 학습 성능 저하 또한 발생할 수 있다.

그래서 여기서 한 가지 소개되는 것이 Double Deep Q Network이다. semi-constant인 label을 사용하는 것이다. 

방법은 간단하다. Q Network의 사본을 만들어서, 한 개는 계속 업데이트가 되도록 하고, 다른 하나는 그대로 남아있도록 하는 방법을 사용할 수 있다. 그리고 상수로 사용하는 네트워크는 가끔씩만 새로 학습된 네트워크로 업데이트를 해주는 것이다. semi-constant라는 이름은 이러한 이유로 붙게되었다. 이 때, 목적함수는 다음과 같다.

$$ Cost = \left[ Q(s,a ; \theta) - \left( r(s,a) + \gamma \max\limits_{a} Q(s^{'}, a ; \Theta) \right) \right]^{2}$$

여기서 $\Theta$는 semi-constant parameter이고, $Q(s^{'}, a ; \Theta)$는 semi-constant Network가 계산해 출력한 Q-value 값을 나타낸다.