[yongggg's] Graph Convolution (Neural) Networks : GCNs

안녕하세요 이번 시간에는 Graph Convolution (Neural) Networks인 GCN에 대해 알아보겠습니다.

Graph Convolutional Networks for Text Classification 논문을 소개하는 과정에서 GCN에 대한 개념을 같이 정리했을 때, 내용이 너무 길어져서 하나의 소주제로 분리를 시켰습니다 ^-^

이 글을 읽고 GCN에 대해 더욱 자세 공부하고 싶으신 분은 GCN의 최초 논문인

Semi-Supervised Classification with Graph Convolutional Networks -Thomas N. Kipf, Max Welling

 

이 paper를 읽는 것을 추천드립니다. 그럼 Graph 이론 부터 GCN 까지 설명 시작하겠습니다!

 

Graph Theory

Graph는 자료구조의 일종으로 Node와 Edge로 표현된다는 고유한 특성을 갖고있다.

Graph는 G는 $ G=(V, E) $로 표현할 수 있으며, $ V (Vertex)$는 node 들의 집합을 의미하며, $ E (Edge) $는 edges의 집합을 의미한다. 

예를 들어, [그림 1]의 Grpah는 다음과 같이 나타낼 수 있다.

• $G = (V, E)$
• $V = {v_{1}, v_{2}, v_{3}, v_{4}, v_{5}} $
• $E = {e_{1} : (v_{1}, v_{2}), e_{2} : (v_{2}, v_{3}), e_{3} : (v_{2}, v_{4}), e_{4} : (v_{3}, v_{5})} $

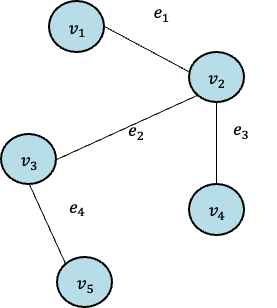
[그림 1] example of Graph

부가적으로, 각 node는 그 자신만의 특성을 갖고 있을 것이며, 이를 feature vector로 표현할 수 있다.

또한 edge 정보는 단순히 연결이 되었는지 안되었는지가 아닌 어느 강도로 연결되어 있는지에 대한 weight 정보까지 담길 수 있다. 

Definition of GCNs

GCNs은 각 node의 정보를 업데이트할 때, 해당 node(*)와 edge로 연결된 이웃 node만의 정보를 반영하여 해당 node(*)를 업데이트하는 연산이다. 이를 수식과 예시를 통해 알아보자.

먼저, GCNs 연산을 위한 정의들은 다음과 같다.

• $ G = (V, E) $
• $ A \in R^{n \times n}$ : Adjacency Matrix of G (nodes의 연결 상태를 0과 1로 나타낸 matrix)
• $ D \in R^{n \times n}$ : Degree Matrix ($D_{ii} = \sum_{j} A_{ij}$)
• $ \tilde{A} \in R^{n \times n}$ : Normalized symetric adjacency matrix ($ D^{-1/2}AD^{-1/2} $)
• $ X \in R^{n \times m} $ : Feature Matrix (nodes가 갖고 있는 특성을 담음)
• $ W \in R^{m \times k}$ : Weight Matrix (학습 Parameter)

여기서 Adjacency Matrix를 Normalize한 $ \tilde{A} $ Matrix는 각 node에 연결된 edge의 개수에 따라 인접행렬을 정규화하는 것인데, 이는 노드의 정보량을 정규화 하기 위함이다. 이렇게 정규화를 했을 때, 각 node별 edge의 갯수에 관련없이 모든 node들을 잘 학습할 수 있다.

이제 위의 matrix들을 가지고 GCN 연산을 수행할 수 있다. Graph data가 GCN Layer 한 개를 통과했을 때의 output은 다음과 같다.

$$ L^{(1)} = \rho (\tilde{A}XW_{0}) $$

Calculations of GCNs

이 연산이 왜 주변 노드만을 가지고 해당 node(*)를 업데이트 하는지 예시를 들어 알아보자.

먼저, [그림 1]의 Graph의 Adjacency Matrix, Degree Matrix, Feature Matrix, 그리고 Weight Matrix는 다음과 같다.

 

$ A = \begin{bmatrix} 1&1&0&0&0 \\ 1&1&1&1&0 \\ 0&1&1&0&1 \\ 0&1&0&1&0 \\ 0&0&1&0&1 \end{bmatrix}$, $ D = \begin{bmatrix} 2&0&0&0&0 \\ 0&4&0&0&0 \\ 0&0&3&0&0 \\ 0&0&0&2&0 \\ 0&0&0&0&2 \end{bmatrix}$, $\tilde{A} = \begin{bmatrix} 0.5&0.35&0&0&0 \\ 0.35&0.25&0.29&0.35&0 \\ 0&0.29&0.33&0&0.41 \\ 0&0.35&0&0.5&0 \\ 0&0&0.41&0&0.5 \end{bmatrix}$

 

$X= \begin{bmatrix} f_{11}&\cdots&f_{1m} \\ \vdots&\ddots&\vdots \\ f_{51}&\cdots&f_{5m} \end{bmatrix}$, $W= \begin{bmatrix} w_{11}&\cdots&w_{1k} \\ \vdots&\ddots&\vdots \\ w_{m1}&\cdots&f_{mk} \end{bmatrix}$

 

이제, $\tilde{A} X $ 연산을 살펴보자. $v_{1}$을 업데이트 한다고 가정했을 때, $\tilde{A}$행렬의 첫 번째 행 ($ \begin{bmatrix} 0.5&0.35&0&0&0 \end{bmatrix} $)과 $X$ 행렬과 연산이 될 것이다. 이 ($ \begin{bmatrix} 0.5&0.35&0&0&0 \end{bmatrix} $) 행은 3, 4, 5 원소가 0이므로 정확히 $ X$의  1행과 2행과만 연산이 이루어진다. 이 것이 의미적으로는 $v_{1}$(자기 자신 node) 와 $v_{2}$ (이웃 node)만을 가지고 $v_{1}$ node를 업데이트 한다고 할 수 있다.

마찬가지로, $v_{2}, v_{3}, v_{4}, v_{5}$ node들도 다음 과정을 통해 이웃 node만을 가지고 feature가 업데이트 되어진다.

 

다음 과정은 $\tilde{A} X$ 와 $W$의 곱 연산이다. 이는 업데이트된 node의 feature를 학습 가능한  W (parameter)로 목적 함수에 알맞게 중요한 feature에 대한 가중치를 조절하면서 학습이 가능하도록 하며, 최종 $\tilde{A}XW \in R^{5 \times k}$는 k차원으로 정보가 업데이트 된 5개의 node 정보 matrix를 뜻한다.

 

마지막으로 비선형 함수인 activation function을 거치며 최종 output을 산출한다.

 

이런 연산들은 반복하는 것이 N개의 GCNs layer를 거쳤다고 말하고, 이를 수식으로 다음과 같이 나타낼 수 있다.

$$ L^{(N)} = \rho(\tilde{A}L^{(N-1)}W_{j}) $$

---

이렇게 GCNs의 연산 과정을 수식과 예시를 통해 알아보았습니다. 위의 인용한 논문의 내용을 제가 이해한 대로 설명을 해보았는데, 잘 이해가 되셨는지 모르겠습니다..ㅎㅎ 혹시 잘못된 내용이나 추가할 내용, 질문 사항 등이 있으시면 댓글로 남겨주세요! 

긴 글 읽어주셔서 감사합니다!